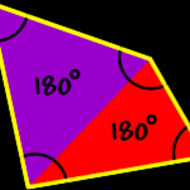
Besides having four sides and four angles, there is a property concerning its quadrilateral interior angle sum 360 degrees. To find the sum of the interior angles of a quadrilateral, we can use the formula again. this time, substitute 4 angles of a interior quadrilateral for n. we find that the sum of the interior angles of a . In the quadrilateral above, one of the angles marked in red color is right angle. by internal angles of a quadrilateral theorem, "the sum of the measures of the interior angles of a quadrilateral is 360°" so, we have. 60 ° + 150° + 3x° + 90° = 360° 60 + 150 + 3x + 90 = 360. simplify. 3x + 300 = 360.
The sum of the interior angles of a quadrilateral equals 360° each of the interior angles in a polygon are equal in measure. 40. question 16. 128. 6. question 17. 79. question 18. 80. question 19. 40. question 20. 60. question 21. There are two triangles because the sum of the angles of each triangle is 180 degrees we get. so, the sum of the interior angles of a quadrilateral is 360 degrees. regular quadrilaterals squares: the properties of squares: all sides are the same length (congruent) and all interior angles are the same size (congruent). The sum of interior angles in a quadrilateral is 360°. this fact is a more specific example of the equation for calculating the sum of the interior angles of a polygon: \[\text {sum of interior.

Angle Measures Of Polygons Assignment And Quiz Flashcards
Free quadrilateral angles calculator calculate the angles of a quadrilateral step by step this website uses cookies to ensure you get the best experience. by using this website, you angles of a interior quadrilateral agree to our cookie policy. Quadrilaterals are four sided polygons, with four vertexes, whose total interior angles add up to 360 degrees. the most common quadrilaterals are the rectangle, .
See more videos for interior angles of a quadrilateral. So, the sum of the interior angles of a quadrilateral is 360 degrees. angles of a interior quadrilateral red line. regular quadrilaterals squares: the properties of squares: squares. all . quadrilateral and its midpoints, then create an inscribed quadrilateral then ask the students to measure the angles sides etc. of inscribed shape and use the measurements to classify the shape( parallelogram ) p olygons interior angles of polygon worksheet exterior angles of a polygon p roving triangles congruent side angle side
The quadrilateral sum conjecture tells us the sum of the angles in any convex quadrilateral is 360 degrees. remember that a polygon is convex if each of its interior angles is less that 180 degree. in other words, the polygon is convex if it does not bend "inwards". Dec 18, 2014 quadrilateral into two triangles 1:22 sum of angles of a triangle is 180 degrees 2:14 sum of the interior angle of a quadrilateral is 360 degrees .
The following diagrams show that the sum of interior angles of a quadrilateral is 360° and the sum of exterior angles of a quadrilateral is 360°. scroll down the page for more examples and solutions on how to find interior and exterior angles of quadrilaterals. da: 81 pa: 94 moz rank: 8. interior angles of a quadrilateral worksheet. The precise statement of the conjecture is: conjecture (quadrilateral sum ): the sum of the measures of the interior angles in any convex quadrilateral is 360 . So, the sum of the interior angles of a quadrilateral is 360 degrees. regular quadrilaterals squares: the properties of squares: all sides are the same length (congruent) and all interior angles are the same size (congruent). to find the measure of the interior angles, we know that the sum of all the angles is 360 degrees (from above).
The interior angles of a quadrilateral (polygon with 4 sides and angles) sum to 360 degrees. we can find this in a couple of ways. first, noting the general formula for an n-gon: s = (n 2)(180) where s is the sum of the interior angles in degrees and n is the number of sides of the n-gon. we find s = (4 2)(180) = 360 degrees. second, the exterior angles must average 360/n degrees. The sum of interior angles in a quadrilateral is 360°. this fact and the properties of quadrilaterals can be used to calculate angles. example. find angle \(d\). \[d = 360 100 70 30 = 160. A quadrilateral has: four sides (edges) four vertices (corners) interior angles that add to 360 degrees: try drawing a quadrilateral, and measure the angles. they should add to 360° types of quadrilaterals. there are special types of quadrilateral: some types are also included in the definition of other types!.
The sum of interior angles in a quadrilateral is 360°. this fact is a more specific example of the equation for calculating the sum of the interior angles of a polygon :. Because the figure shown above is a closed figure and it is covered by four segments, it is quadrilateral. by internal angles of a quadrilateral theorem, "the sum of the measures of the interior angles of a quadrilateral is 360°". so, we have. 82 ° + (25x 2)° + (20x 1)° + (25x + 1)° = 360°. The sum of the interior angles of any quadrilateral is 360°. consider the two examples below. you could draw many quadrilaterals such as these and carefully .
The sum of the interior angles of a quadrilateral are equal to 360 o. to find the fourth angle of a quadrilateral when the other three angles are known, subtract the number of degrees in the other three angles from 360 o.. example: how many degrees are in the fourth angle of a quadrilateral whose other three angles are 80 o and 110 o and 95 o? answer: 360 o 80 o 110 o 95 o = 75 o. So we can use this pattern to find the sum of interior angle degrees for even 1,000 sided polygons. of course it would take forever to do this though. :) reply. Polygons quadrilaterals. so, the sum of the interior angles of a quadrilateral is 360 degrees. all sides are the same length (congruent) and all interior angles are the same size (congruent). to find the measure of the interior angles, we know that the sum of all the angles is 360 degrees (from above).
Polygons Polygon Basics In Depth Math Com
(exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior. do you need homework help interest, interest rate, interior angles, intersection, intersection of sets, inverse cosine, inverse functions, inverse matrix, inverse quadratic equations, quadratic formula, quadratic fromula, quadratic inequalities, quadrilaterals, quart, middle school math live online tutoring on quotient, quotient rule, radian, radian measure help you can also print radical equations worksheets, radical expressions, radical functions, radicals, high school math do you need homework help radius, range, range of a function, rate, rate equations video clips, ratio, high Interior angles of polygons. an interior angle is an angle inside a shape. interior exterior angles. another example: interior exterior angles . (exercise: make sure each triangle here adds up to 180°, and check that the pentagon's interior angles add up to 540°) the interior angles of a pentagon add up to 540° the general rule. each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total:.
No comments:
Post a Comment